🔬 AI for Scientific Discovery
This page highlights ongoing and past research efforts connecting AI, symbolic systems, and scientific discovery at the reasoning and learning research group @ Georgia Tech led by Professor Vijay Ganesh.
Towards Certificate-Driven Software Porting: A Self-Improving Agentic Harness for Scientific Program Optimization (2026)
Authors: Piyush Jha1, Aishik Ghosh1,2, Vijay Ganesh1
Affiliations: 1Georgia Institute of Technology, USA | 2Lawrence Berkeley National Laboratory, USA
TL;DR: Certificate-Driven Evolutionary Search (CDES) turns failed program candidates into reusable restrictions that guide LLM-based search through rejection, backtracking, and targeted repair. Applied to CPU-to-GPU translation of two Geant4 particle-simulation functions, a harness combining formal, numerical, physics, and GPU safety checks yields 13.78× and 23.54× function-level speedups over CPU code, including data conversion and transfers.
CDRL: Certification-Driven Reinforcement Learning for Neutrino Flavor Model Discovery (2026)
Authors: Piyush Jha1, Jake Rudolph2, Victoria Knapp-Pérez2,5, Max Fieg3, Aishik Ghosh1,4, Vijay Ganesh1
Affiliations: 1Georgia Institute of Technology, USA | 2University of California, Irvine, USA | 3Fermilab, USA | 4Lawrence Berkeley National Laboratory, USA | 5Halluminate, USA
TL;DR: CDRL combines reinforcement learning with symbolic reasoning to discover neutrino flavor models. Certificates explaining failed candidates become reusable logical constraints that prune invalid regions of the search space. Across three theory spaces, it achieves up to 6.33× higher neutrino model discovery rates while evaluating up to 4× fewer candidates than the prior RL approach, and extracts interpretable rules for future searches.
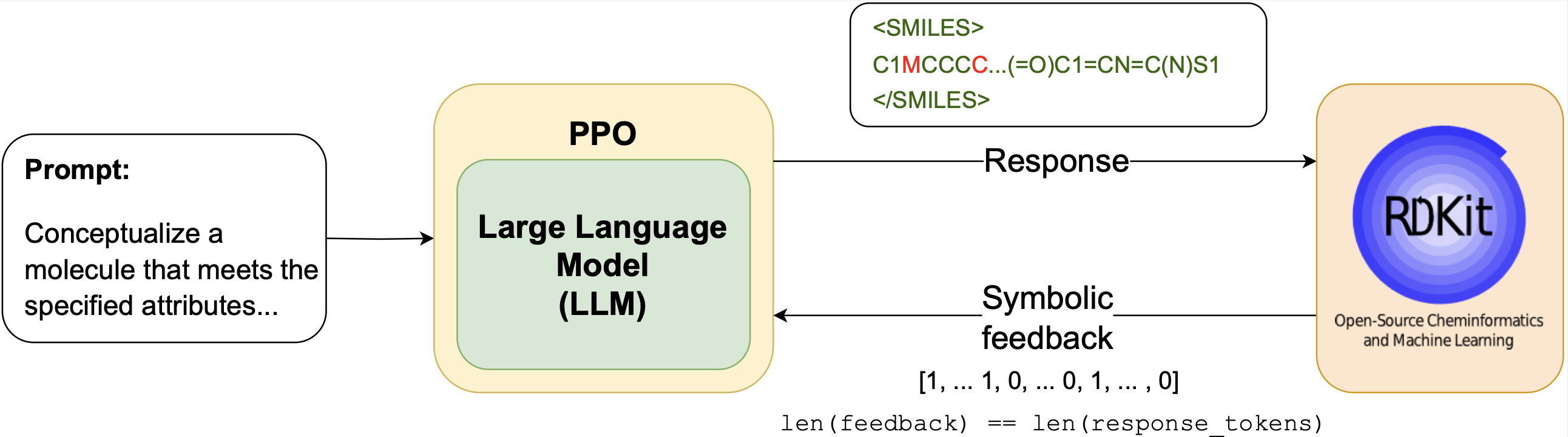
Reinforcement Learning via Symbolic Feedback (RLSF) – Chemistry
Authors: Piyush Jha1, Prithwish Jana1, Pranavkrishna Suresh1, Arnav Arora1, Vijay Ganesh1
Affiliations: 1Georgia Institute of Technology, USA
TL;DR: RLSF introduces a new way to fine-tune LLMs for molecular design and synthesis by combining reinforcement learning with token-level symbolic feedback from cheminformatics tools such as RDKit. Fine-grained chemical error signals (e.g., valence violations, missing functional groups) drive a PPO loop to iteratively improve the LLM; the approach extends to materials science and physics discovery.
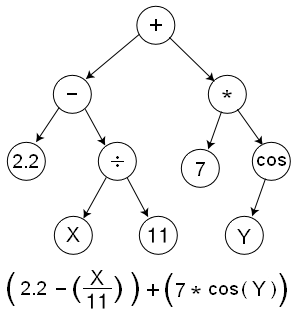
Symbolic Density Estimation Through Symbolic Regression: A Decompositional Approach
Authors: Angelo Arvind Rajendram1, Xieting Chu2, Aishik Ghosh2, Max Fieg3, Vijay Ganesh2
Affiliations: 1University of Waterloo, Canada | 2Georgia Institute of Technology, USA | 3University of California, Irvine, USA
TL;DR: The AI-Kolmogorov Framework decomposes high-dimensional density estimation via clustering and structure learning, then applies symbolic regression to marginal and conditional distributions to recover interpretable analytic models and rediscover underlying distributions.
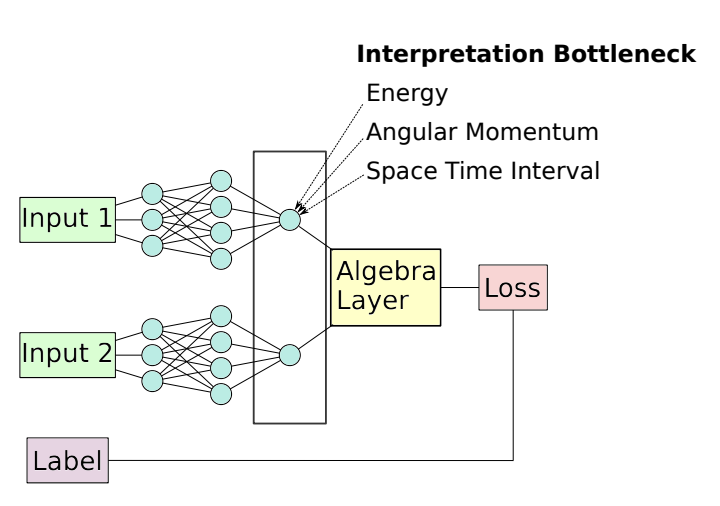
Discovering Laws of Physics via Interpretable Siamese Neural Networks
Authors: Sebastian J. Wetzel1, Roger G. Melko1,2, Joseph Scott2, Maysum Panju2, Vijay Ganesh2
Affiliations: 1Perimeter Institute for Theoretical Physics, Canada | 2University of Waterloo, Canada
TL;DR: Interpretable Siamese Neural Networks learn to identify symmetry invariants and conserved quantities by clustering similar physics events—without prior domain knowledge—across settings like special relativity and electromagnetic field transformations.
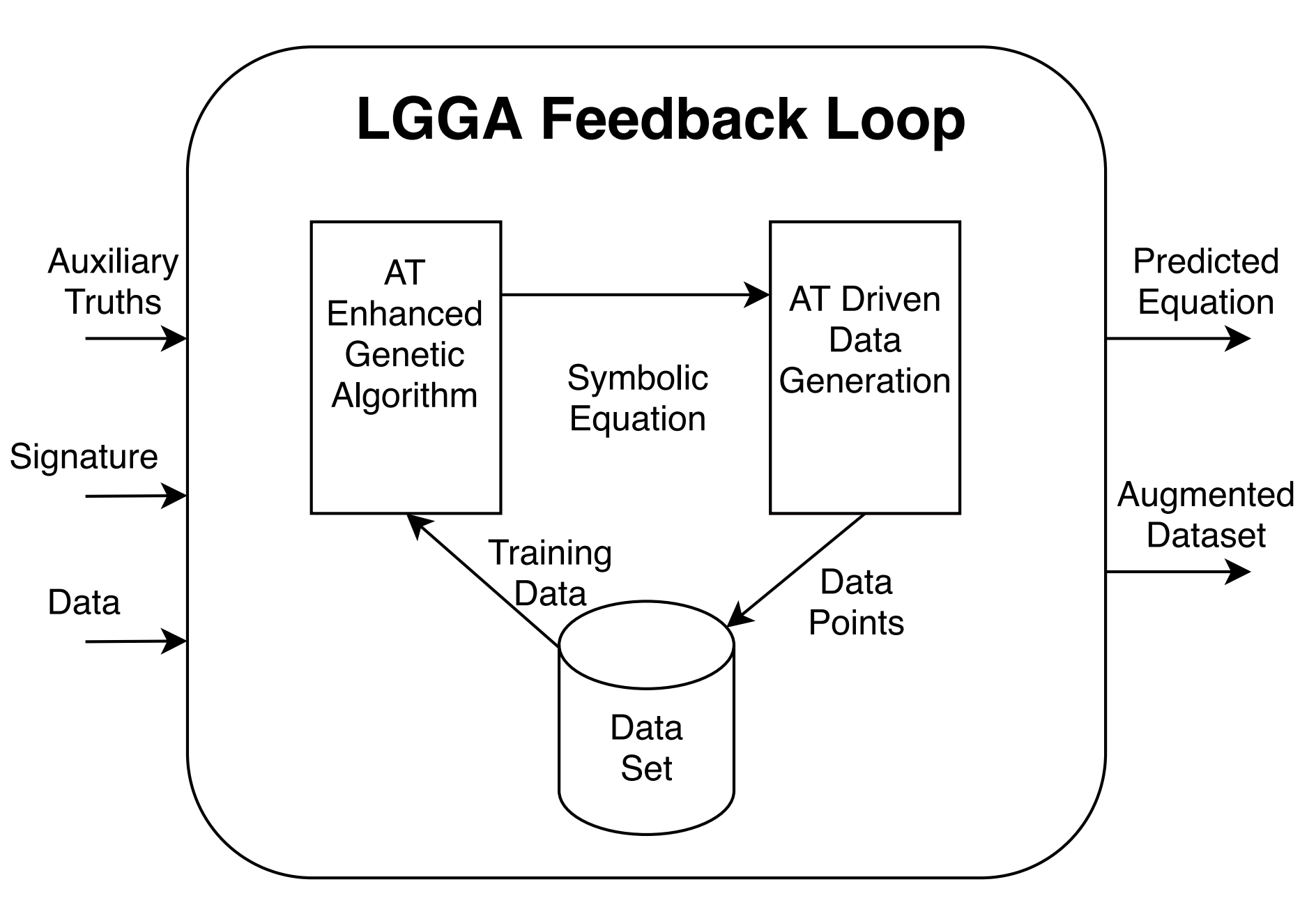
Logic Guided Genetic Algorithms (LGGA)
Authors: Dhananjay Ashok1, Joseph Scott2, Sebastian J. Wetzel3, Maysum Panju2, Vijay Ganesh2
Affiliations: 1University of Toronto, Canada | 2University of Waterloo, Canada | 3Perimeter Institute for Theoretical Physics, Canada
TL;DR: LGGA augments symbolic regression with auxiliary truths (known domain facts) in both scoring and data augmentation to dramatically improve data efficiency in equation discovery.
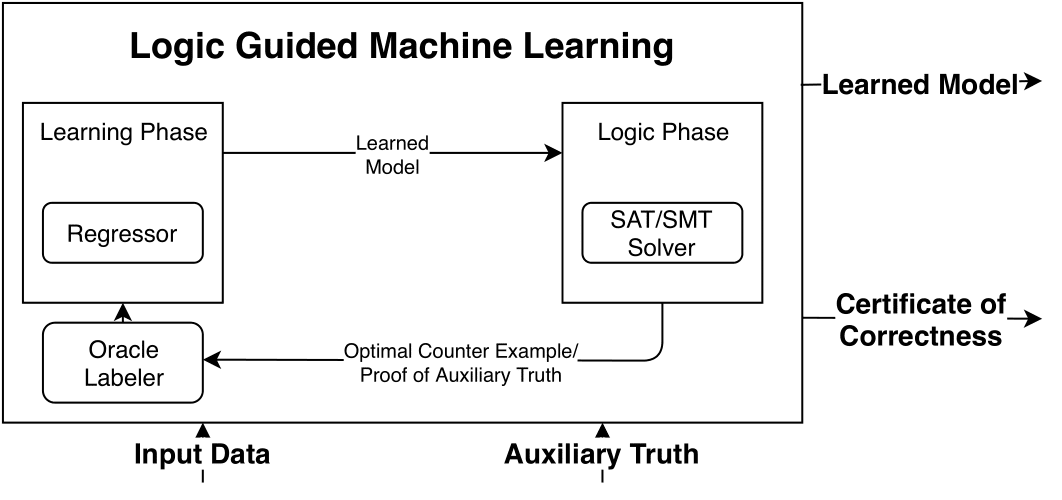
Logic Guided Machine Learning (LGML)
Authors: Joseph Scott1, Maysum Panju1, Vijay Ganesh1
Affiliations: 1University of Waterloo, Canada
TL;DR: LGML combines a learning model that proposes symbolic expressions from data with a logic solver that checks consistency against auxiliary truths, returning counterexamples to guide a feedback loop and yield highly data-efficient learning of core expressions.