AlphaMapleSAT

Overview

Authors: Piyush Jha^†,1, Zhengyu Li^†,1, Zhengyang (John) Lu², Curtis Bright³, Vijay Ganesh¹

Affiliations: ¹Georgia Institute of Technology, USA  |  ²University of Waterloo, Canada  |  ³University of Windsor, Canada

^† Equal contributions

arXiv Code: AlphaMapleSAT Code: Parallel CnC Runner

TL;DR

AMS integrates Monte Carlo Tree Search (MCTS) with deductive feedback—using propagation rate via unit propagation—in the Cube-and-Conquer paradigm to guide cubing. By focusing exploration on promising cubes it reduces wasted work and achieves up to an 8× wall-clock speedup versus March on the hardest Kochen–Specker and Ramsey instances.

Key ideas

• MCTS-guided cubing with deductive rewards (propagation rate via unit propagation) to prioritize promising branches.
• PUCT-based selection without neural nets; priors from BCP counts.
• Boolean Constraint propagation (BCP) feedback from deeper exploration improves partition quality.
• Keeps cubing costs low with lightweight simplification and incremental solving.

Pipeline (summary)

• Input: CNF formula
• Cubing: MCTS + deductive rewards to generate cubes
• Conquer: solve cubes in parallel with CDCL workers
• Output: SAT / UNSAT

Results snapshot

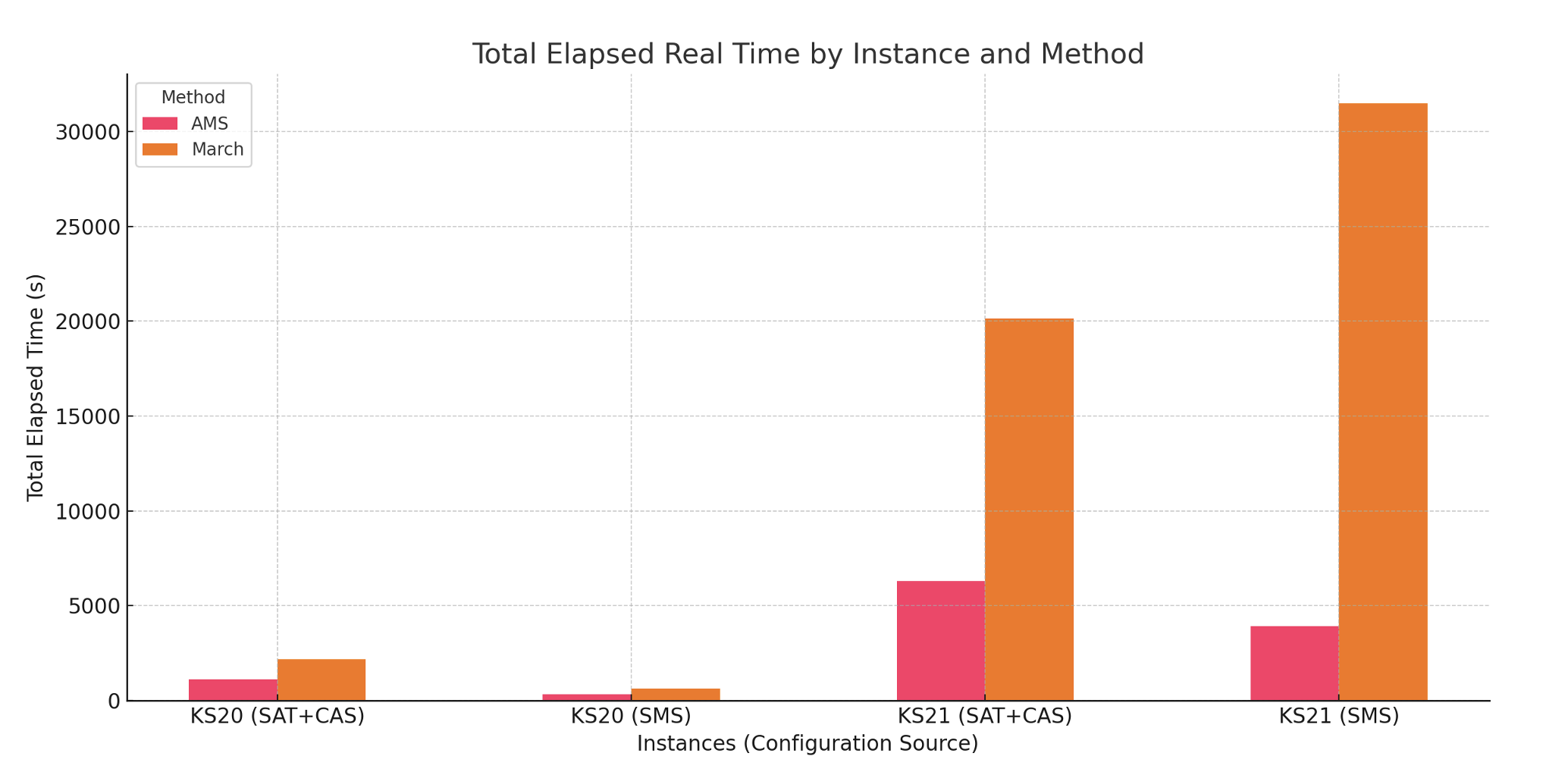
We evaluated AMS on challenging benchmarks such as the Kochen–Specker and Ramsey problems. The bar chart above shows total elapsed wall-clock time per instance (AMS in pink, March in orange). AMS achieves up to an 8× end-to-end speedup on the hardest instances.

Key takeaways